Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach of differential calculus to solving a problem with constraints. One might think, in analogy, of a structure that is not completely rigid, and that deforms slightly to accommodate forces applied from the outside; this explains the name.
Some characteristic phenomena are: the derivation of first-order equations by treating the ε quantities as having negligible squares; the possibility of isolated solutions, in that varying a solution may not be possible, or does not bring anything new; and the question of whether the infinitesimal constraints actually 'integrate', so that their solution does provide small variations. In some form these considerations have a history of centuries in mathematics, but also in physics and engineering
There are lot of studies which are involved with the investigation about deformation theory .Some simple one are summarized as following:
Material Behaviour in Metal Forming
Plastic region of stress-strain curve is primary interest because material is plastically deformed In plastic region, metal's behaviour is expressed by the flow curve:
σ = Kε n
where K = strength coefficient; and n = strain hardening exponent
Average Flow Stress
It is determined by integrating the flow curve equation between zero and the final strain value defining the range of interest
σ= K x εnm/1+n where εm = maximum strain during deformation process Tensile Test – Load-Displacement Diagram
The tensile test can be a deformation process therefore the date from this test can be useful for deformation process. Figure 1 shows the elastic deformation of a sample and the useful data.
Figure 2 shows the Stress determination depending on Load (Elastic Deformation).
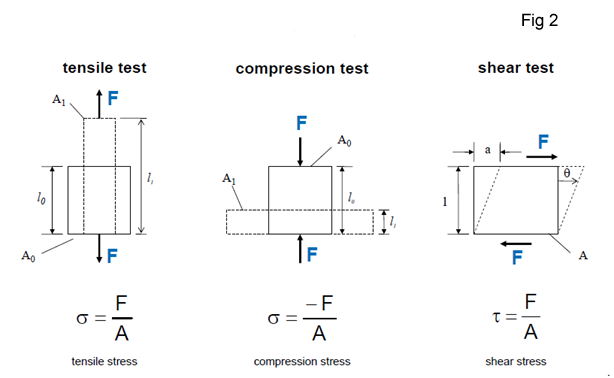
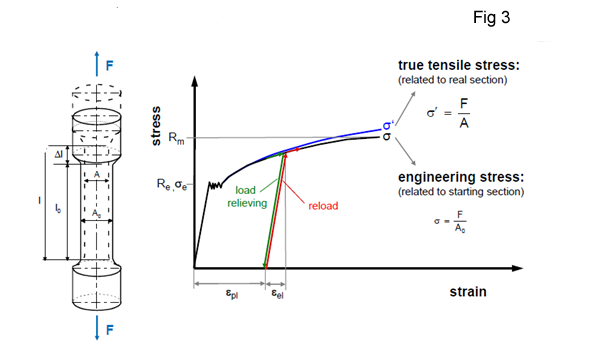
Figure 3 shows Stress –strain Curve up to the Uniform Elongation (Plastic Deformation).